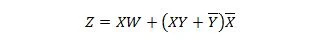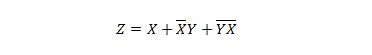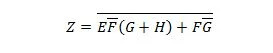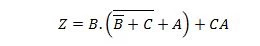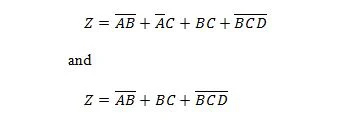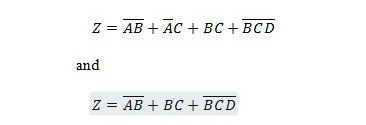Luku 2: Boolen algebra ja siihen liittyvät tietokonekomponentit
2.1 Boolen perusoperaattorit
Oletetaan, että minä (kirjoittaja) olen pitkä ja sinä (lukija) olet pitkä. Jos joku kysyy sinulta, olemmeko molemmat pitkiä, vastaat 'Kyllä' (tosi). Jos hän kysyy, olemmeko molemmat lyhyitä, vastaat 'Ei' (väärä). Jos olet lyhyt ja minä pitkä, ja hän kysyy, oletko sinä vai minä pitkä, vastauksesi olisi 'Kyllä' (tosi). Jos hän kysyy, oletko sinä ja minä pitkiä, et saa vastausta. Voit jatkaa sanomalla, että viimeistä kysymystä ei pidä esittää tai että kysymykseen ei ole vastausta. No, haluan sinun (lukijan) tietävän, että tänään, tietyissä olosuhteissa, kysymys pitäisi esittää.
Biologiassa ihminen on joko pitkä tai lyhyt. Juuri 'ympäristöolosuhteet' tekevät ihmisestä keskipitkän. Eräs tiedemies, George Boole, määritteli joukon vastauksia tai sääntöjä tällaisille kysymyksille. Opimme nämä säännöt tässä online-urakurssin osiossa (luku). Näitä sääntöjä käytetään nykyään tietojenkäsittelyssä, ohjelmoinnissa, elektroniikassa ja tietoliikenteessä. Itse asiassa ilman näitä sääntöjä sinulla ei olisi tietokonetta, kuten se on yleistä nykyään; sinulla ei myöskään olisi ohjelmointia, kuten se on yleistä nykyään.
Totta vai tarua
Yksinkertainen ihmiskielinen lausunto on joko tosi tai epätosi sinänsä. Jos sanon: 'Olen pitkä', se on joko totta tai tarua. Jos sanon 'olet pitkä', se on joko totta tai tarua. Jos minä olen pitkä ja sinä lyhyt, ja kysytään, oletko sinä ja minä pitkiä, Boolen logiikassa on annettava vastaus tosi tai epätosi. Kumpi näistä kahdesta pitäisi antaa? Boole ei oikeastaan vastannut tähän kysymykseen. Hän vain keksi joukon sääntöjä, joita meidän on noudatettava. Hyvä uutinen on, että kun noudatat näitä sääntöjä oikeassa kontekstissaan, sinulla ei ole epäselvyyttä. Näiden sääntöjen ansiosta meillä on nykyään tietokoneita ja ohjelmointia. Säännöt on nyt annettu sinulle. Sääntöjä ei voi oikeastaan selittää; sinä vain hyväksyt ne. Säännöt ovat kolmen otsikon alla: JA, TAI ja EI.
JA
Kysymys voidaan esittää, jos sekä sinä että minä olemme pitkiä. Minun pituuteni ja sinun pituutesi yhdistetään sitten JA-säännöillä. Näitä JA-sääntöjä on noudatettava:
false JA false = false
epätosi JA tosi = epätosi
tosi JA epätosi = epätosi
totta JA totta = totta
Olkoon korkea nyt totta ja lyhyt valhetta. Tämä tarkoittaa, että jos minä olen lyhyt JA sinä olet lyhyt, sinä ja minä olemme lyhyitä. Jos minä olen lyhyt JA sinä olet pitkä, sinä ja minä olemme lyhyitä; se on Boolen vastaus, joka sinun on hyväksyttävä. Jos minä olen pitkä JA sinä olet lyhyt, sekä sinä että minä olemme lyhyitä. Jos minä olen pitkä JA sinä olet pitkä, sinä ja minä olemme pitkiä. Kaikki nämä ovat JA Boolen sääntöjä, jotka sinun (lukijan) on vain hyväksyttävä.
TAI
Kysymys voidaan esittää oletko sinä TAI minä pitkä. Minun pituuteni ja pituutesi yhdistetään sitten TAI-säännöillä. Näitä TAI-sääntöjä on noudatettava:
false TAI false = false
epätosi TAI tosi = tosi
tosi TAI epätosi = tosi
tosi TAI tosi = totta
Jälleen, olkoon pitkä totta ja lyhyt tarua. Tämä tarkoittaa, että jos minä olen lyhyt TAI sinä olet lyhyt, sinä TAI minä olet lyhyt. Jos minä olen lyhyt TAI sinä olet pitkä, sinä tai minä olet pitkä. Jos minä olen pitkä TAI olet lyhyt, sinä TAI minä olen pitkä. Jos minä olen pitkä TAI sinä olet pitkä, sinä tai minä olet pitkä. Kaikki nämä ovat Boolen sääntöjä, jotka sinun on hyväksyttävä.
EI
Nyt Boolen logiikassa on vain kaksi tilaa (mahdollista vastausta). Eli jos ET ole pitkä, olet lyhyt. Jos ET ole lyhyt, olet pitkä; ei mitään muuta. Nämä ovat sääntöjä, joita EI tarvitse noudattaa:
EI väärin = totta
EI totta = epätosi
Oletetaan, että sinulla on naru (tai jousi), jota voit pidentää (vetää). Kun merkkijono on luonnollisessa tilassaan, jos sanon 'EI lyhyt', jatkaisit sitä; se on tulkinta. Kun merkkijonoa on jatkettu, jos sanon 'EI pitkä', antaisit sen supistua; se on tulkinta.
Sinun on opittava ulkoa kaikki annetut säännöt niiden eri luokissa.
Enemmän kuin kaksi operandia
Tietokonekielessä AND, OR ja NOT kutsutaan kutakin operaattoriksi. NOT-operaattorille tarvitset vain yhden operandin (arvon operaattorille) saadaksesi vastauksen. AND- tai OR-operaattoreilla voi olla enemmän kuin kaksi operandia. Edelliset tapaukset näyttävät kaksi operandia AND:lle ja OR:lle. Sinulla voi olla kolme operandia AND:lle seuraavasti:
epätosi JA epätosi JA false = epätosi
epätosi JA epätosi JA tosi = epätosi
Nämä ovat kaksi riviä; jokaisessa on kaksi AND-operaattoria. Itse asiassa riviä on yhdeksän, kun operandit ovat kolme. AND-operaattorilla vain viimeinen rivi (yhdeksäs rivi) on yhtä suuri kuin tosi; kaikki edelliset rivit ovat vääriä. Huomaa, että kahdella AND-operandilla vain viimeinen rivi on tosi still; kaikki kolme edellistä riviä ovat vääriä. Kun operandit ovat neljä, riviä on 16 ja vain viimeinen rivi on tosi AND-operaattorille.
AND- ja OR-malli ovat erilaisia. Kolmella operandilla kahdelle TAI-operaattorille on myös yhdeksän riviä ja vain ensimmäinen rivi on tällä kertaa epätosi. Toisesta yhdeksänteen riviin on totta. Huomaa, että kahdella OR-operandilla vain ensimmäinen rivi on tosi still; kaikki loput kolme riviä ovat vääriä. Kun OR:n operandit ovat neljä, riviä on myös 16.
NOT-operaattori käsittelee vain yhtä operandia. EI epätosi on totta ja EI tosi on epätosi.
2.2 Kaksi operandin totuustaulukkoa ja niiden elektroniset komponentit
Matematiikassa on aihe nimeltä algebra. Pieni osa siitä nähtiin edellisessä luvussa. On olemassa eräänlainen algebra, jota kutsutaan Boolen algebraksi. Boolen algebrassa tosi tunnistetaan kahdesta kantanumerosta, joka on 1, ja false tunnistetaan kahdesta kantanumerosta, joka on 0.
Tietokoneyksikön sisäiset komponentit ovat elektronisia komponentteja. Tietokonejärjestelmän järjestelmäyksikössä on digitaalisia elektronisia komponentteja. JA-toiminnon suorittaa pieni elektroninen komponentti, nimeltään JA-portti. TAI-toiminnon suorittaa pieni elektroninen komponentti, jota kutsutaan TAI-portiksi. NOT-toiminnon suorittaa pieni elektroninen komponentti, jota kutsutaan NOT-portiksi. Liian monet näistä porteista voivat olla integroidun piirin (IC) sirussa.
JA Totuustaulukko ja sen portti
Seuraavassa taulukossa on AND-totuustaulukko ja sen AND-portin (pieni piiri) symboli:
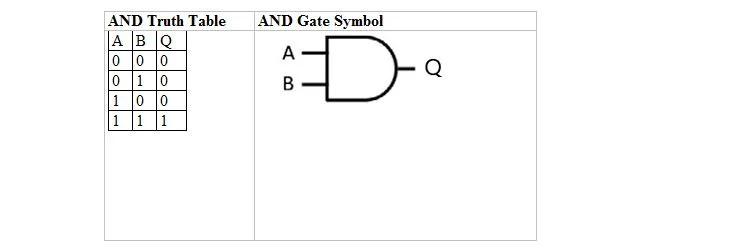
Sekä AND-totuustaulukolle että sen portille A ja B ovat kaksi syötemuuttujaa. Q on lähtömuuttuja. A on joko 1 tai 0. B on joko 1 tai 0. Q on joko 1 tai 0. JA-totuustaulukko, jossa on 1 ja 0, on sama kuin edellinen tosi/epätosi JA totuusasettelu (taulukko). JA-yhtälö on:
A . B = Q
jossa piste (.) tarkoittaa JA (Boolean). Piste voidaan jättää pois, jos siinä on AB = Q, mikä tarkoittaa samaa asiaa (AND).
Huomautus: A:n ja B:n bitit neljällä rivillä pareina ovat kakkosluvun neljä ensimmäistä numeroa alkaen 0:sta (tai 00:sta), eli 00, 01, 10, 11.
Seuraavassa taulukossa on TAI-totuustaulukko ja sen TAI-portin (pieni piiri) symboli:
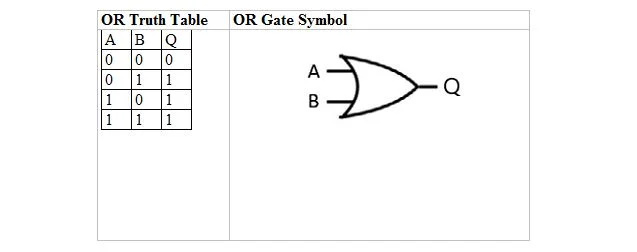
Sekä TAI-totuustaulukolle että sen portille A ja B ovat kaksi syötemuuttujaa. Q on lähtömuuttuja. TAI-totuustaulukko, jossa on 1 ja 0, on sama kuin edellinen tosi/epätosi TAI-totuusasettelu (taulukko).
OR-yhtälö on:
A + B = Q
Missä + tässä tarkoittaa Boolen TAI:ta eikä lisäystä. Yhtälö luetaan 'A tai B yhtä kuin Q'.
Seuraavassa taulukossa on NOT totuustaulukko ja sen EI-portti (pieni piiri) symboli:
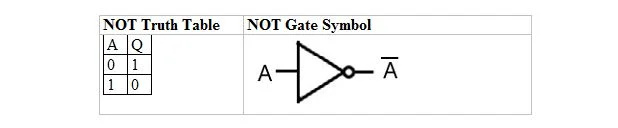
NOT totuustaulukossa tai NOT-portissa on vain yksi tulo ja yksi lähtö. Kun tulo on 0, lähtö on 1. Kun tulo on 1, lähtö on 0. NOT-portti tekee eräänlaisen inversion. Tulosmuuttuja on sama kuin tulomuuttuja, mutta siinä on palkki (yliviivattu). EI totuustaulukko, jossa on 1 ja 0, on sama kuin edellinen tosi/epätosi TAI totuusasettelu (taulukko).
EI-yhtälö on:
A = Q
Missä Q = A ja pylväs A:n päällä tarkoittaa tässä komplementtia. 0:n komplementti on 1 ja luvun 1 komplementti on 0. NOT-portti tunnetaan myös nimellä KÄÄNTÄVÄ portti.
Nämä ovat perustavanlaatuisia (tai juuri) totuustaulukoita ja niiden portteja (pieniä piirejä) digitaalisessa elektroniikassa (Boolen algebralla). Seuraavassa kuvassa olevat kolme muuta totuustaulukkoa ja niiden portit ovat mukavuussyistä ja perustuvat kolmeen edelliseen totuustaulukkoon.
On totuustaulukko ja portti, jotka on johdettu AND totuustaulukosta ja portista. Niitä kutsutaan NAND (for NOT AND) totuustaulukoksi ja vastaavaksi NAND-portiksi. NAND-totuustaulukko ja sen NAND-portti ovat:
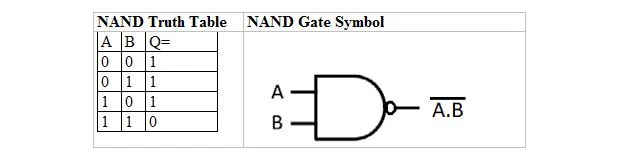
Saadaksesi NAND-totuustaulukon, siirry AND-totuustaulukon ulostuloon ja korvaa jokainen numero sen komplementilla. 0:n komplementti on 1 ja 1:n komplementti on 0. NAND-portti on kuin JA-portti, mutta siinä on pieni ympyrä ennen lähtöriviä. NAND-yhtälö on:
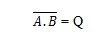
Missä tarkoittaa 'A' ja 'B' tuloksen komplementtia. Palkkia (yliviiva) edustaa portissa pieni ympyrä. Huomaa, että piste A:n ja B:n välillä voidaan jättää pois.
On toinen totuustaulukko ja portti, jotka on johdettu TAI-totuustaulukosta ja -portista. Niitä kutsutaan NOR (for NOT OR) totuustaulukoksi ja vastaavaksi NOR-portiksi. NOR-totuustaulukko ja sen NOR-portti ovat:
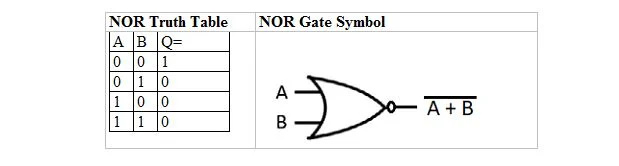
Saadaksesi NOR-totuustaulukon mene TAI-totuustaulukon ulostuloon ja korvaa jokainen numero sen komplementilla. 0:n komplementti on 1 ja luvun 1 komplementti on 0. NOR-portti on kuin TAI-portti, mutta siinä on pieni ympyrä ennen lähtöriviä. NOR-yhtälö on:
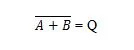
Missä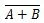 
tarkoittaa 'A' TAI 'B' tuloksen komplementtia. Palkkia (yliviivaa) edustaa portissa pieni ympyrä.
Yksinomainen OR (XOR)
OR-portin totuustaulukko on:
Normaalissa englannin kielessä ei ole selvää, pitäisikö viimeisen rivin 1 TAI 1 antaa 1 vai 0. Joten Boolen algebrassa on kahdenlaisia TAI-totuustaulukoita ja kaksi vastaavaa porttia. Normaalilla TAI:lla viimeinen rivi 1 TAI 1 antaa arvon 1. Toinen TAI-tyyppi on poissulkeva TAI (XOR), jossa kolme ensimmäistä riviä ovat samat kuin normaalin TAI:n kolme ensimmäistä riviä (mukaan lukien tulos). Neljännelle ja viimeiselle riville 1 TAI 1 antaa kuitenkin 0.
Seuraavassa taulukossa on XOR-totuustaulukko ja sen XOR-portin (pieni piiri) symboli:
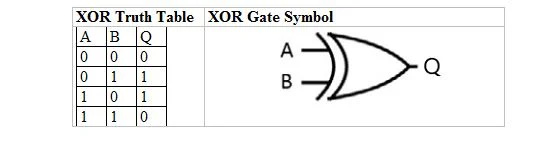
Sekä XOR-totuustaulukolle että sen portille 'A' ja 'B' ovat kaksi syötemuuttujaa. 'Q' on lähtömuuttuja.
XOR-yhtälö on:
A ⊕ B = Q
Missä ⊕ tässä tarkoittaa Boolen XOR:ta.
Normaali TAI tarkoittaa jompaakumpaa tai molempia. Yksinomainen TAI tarkoittaa tiukasti jompikumpi eikä molempia.
2.3 Boolen postulaatit
Postulaatit ovat oletuksia, joiden perusteella tehdään tiettyjä johtopäätöksiä. On olemassa kymmenen Boolen postulaattia, jotka ovat juurtuneet AND-, OR- ja NOT-yhtälöistä (totuustaulukot). Näitä yhtälöitä kutsutaan myös funktioiksi. Perustoiminnot kopioidaan seuraavasti:
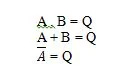
Nämä ovat Boolen algebran perusfunktioita (yhtälöitä). Seuraavat kolme muuta (funktioiden) yhtälöä eivät ole perusfunktioita:
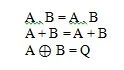
Vaikka viimeinen toiminto tässä on erikoinen, sitä ei pidetä perusfunktiona.
Boolen postulaatit ovat seuraavat:
AND Functionista
1) 0. 0 = 0
kaksikymmentä. 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
OR-funktiosta
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
NOT Functionista
9) 0 = 1
10) 1 = 0
Huomautus: Nämä postulaatit ovat vain rivejä AND-, OR- ja EI-totuustaulukoissa, jotka ilmaistaan itsenäisesti. Lukijan tulee muistaa annetut postulaatit.
2.4 Boolen ominaisuudet
Ominaisuus on kuin ominaisuus jollekin. Boolen ominaisuudet ovat yhtälöitä, jotka on johdettu Boolen postulaateista. Tässä osiossa ominaisuudet annetaan yksinkertaisesti ilman johdannaisia ja niitä käytetään myöhemmin. Ominaisuuksista 25 on ryhmitelty kymmenen otsikon alle seuraavasti:
AND-funktion ominaisuudet
Omaisuus 1:
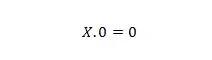
Missä X voi olla 1 tai 0. Tämä tarkoittaa, että riippumatta siitä, mikä X on, tulos on aina 0.
Huomaa: Muuttujan ei välttämättä tarvitse olla A tai B tai C tai D. Muuttuja voi olla W tai X tai Y tai Z tai mikä tahansa muu kirjain.
Omaisuus 2:
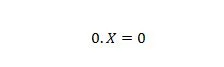
Missä X voi olla 1 tai 0. Huomaa, että ominaisuuden 1 ja ominaisuuden 2 välinen ero on se, että molempien yhtälöiden yhtäläisyysmerkin vasemmalla puolella X:n ja 0:n paikat vaihdetaan.
Omaisuus 3:
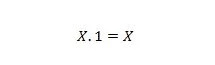
Jos X on 0, niin 0. 1 = 0. Jos X on 1, niin 1. 1 = 1.
Omaisuus 4:
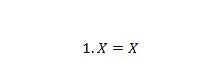
Jos X on 0, niin 1. 0 = 0. Jos X on 1, niin 1. 1 = 1. Huomaa, että ominaisuuden 3 ja ominaisuuden 4 välinen ero on se, että molempien yhtälöiden vasemmalla puolella X ja 1 vaihdetaan keskenään.
OR-funktion ominaisuudet
Omaisuus 5:
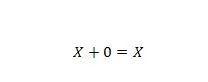
Missä X voi olla 1 tai 0. Tämä tarkoittaa, että jos X on 0, tulos on 0. Jos X on 1, tulos on 1.
Omaisuus 6:
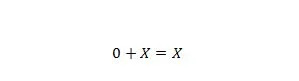
Missä X voi olla 1 tai 0. Huomaa, että ominaisuuden 5 ja ominaisuuden 6 välinen ero on se, että molempien yhtälöiden vasemmalla puolella X:n ja 0:n paikat vaihdetaan.
Omaisuus 7:
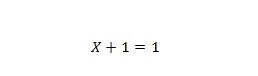
Jos X on 0, niin 0 + 1 = 1. Jos X on 1, niin 1 + 1 = 1.
Kiinteistö 8:
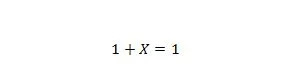
Jos X on 0, niin 1 + 0 = 1. Jos X on 1, niin 1 + 1 = 1. Huomaa, että ominaisuuden 7 ja ominaisuuden 8 välinen ero on se, että molempien yhtälöiden vasemmalla puolella X ja 1 vaihdetaan keskenään.
Ominaisuudet, jotka liittyvät muuttujan yhdistämiseen itsensä tai sen täydennyksen kanssa
Kiinteistö 9: 
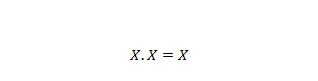
Eli: jos X on 0, niin 0. 0 = 0. Jos X on 1, niin 1 . 1 = 1.
Omaisuus 10:
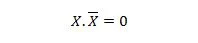
Eli: jos X on 0, niin 0. 1 = 0. Jos X on 1, niin 1. 0 = 0.
Peräkkäisille muuttujille tästä ominaisuudesta tulee:
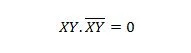
Kiinteistö 11:
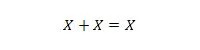
Eli: jos X on 0, niin 0 + 0 = 0. Jos X on 1, niin 1 + 1 = 1 (normaalista TAI).
Kiinteistö 12:
Eli: jos X on 0, niin 0 + 1 = 1. Jos X = 1, niin 1 + 0 = 1.
Eli: jos X on 0, niin 0 + 1 = 1. Jos X = 1, niin 1 + 0 = 1.
Kaksinkertainen täydennys
Kiinteistö 13:
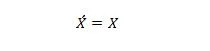
Kun vasemman puolen X on 0, oikean puolen X on 0. Kun oikean puolen X on 1, vasemman puolen X on 1. Toisin sanoen, kaksoiskomplementit palauttaa alkuperäisen arvon.
Kommutatiivinen laki
Kiinteistö 14:
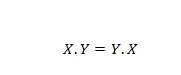
Tämä tarkoittaa, että ensimmäisen ja toisen operandin vaihtamisella AND-operaattorille yhtäläisyysmerkin vasemmalla puolella ei ole merkitystä; vastaus on edelleen sama, kun vasemman puolen vaihto on tapahtunut. Tämä yhtälö voidaan kirjoittaa pisteet jättämällä pois seuraavasti: XY = YX.
Kiinteistö 15:
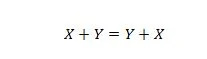
Selitys tässä on sama kuin edellisessä JA, mutta se on OR-operaattorille.
Jakelulaki
Kiinteistö 16:
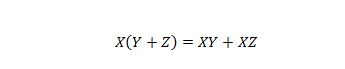
Tässä on kolme muuttujaa: X, Y ja Z. Jokainen muuttuja voi olla joko 1 tai 0. Tasa-arvosymbolin vasemmalla puolella suluissa on tarkoitus arvioida ensin, mitä niissä on. Sitten JA on tulos X:llä. Oikea puoli sanoo, että X JA Y yhdessä TAI X JA Z yhdessä ovat samat kuin vasen puoli. Huomaa, että AND-merkkien pisteoperaattori jätetään kokonaan pois; ja yhdistetyt muuttujat tarkoittavat edelleen JA.
Kiinteistö 17:
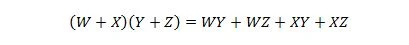
Tämä ominaisuus on ominaisuuden 16 laajennus, johon on lisätty muuttuja W.
Yhdistyslaki
Kiinteistö 18:
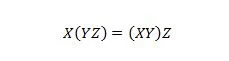
Suluissa on ensin arvioitava, mitä suluissa on. Jos siis vasemman puolen lausekkeelle Y ja Z ovat AND-etuja ja X on AND-tuloksen kanssa, niin vasemman puolen lopputulos on sama kuin oikealla oleva lopputulos. -käsipuoli, jossa X ja Y on AND-edettu ensin ennen AND-tulosta Z:lla. Huomaa, että pisteet on jätetty pois yhtälöstä.
Kiinteistö 19:
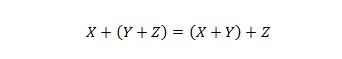
Tämä ominaisuus selitetään samalla tavalla kuin ominaisuus 18, mutta OR-operaattoria käytetään AND-operaattorin sijaan. TAI-operaattoria + ei koskaan jätetä pois Boolen lausekkeesta yksinkertaisuuden vuoksi. Toisaalta AND-operaattori voidaan jättää pois ja kaksi muuttujaa voidaan yhdistää.
Imeytyminen
Kiinteistö 20:
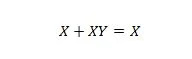
Tällä yhtälöllä, riippumatta siitä, mikä Y on, oikea puoli on aina X (absorboitu).
Kiinteistö 21:
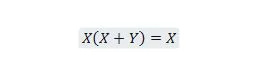
Lisäksi tällä yhtälöllä, riippumatta siitä, mikä Y on, oikea puoli on aina X (absorboitu). Tämä ominaisuus 21 on sama kuin ominaisuus 20, joka on:
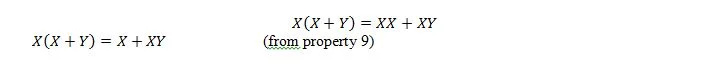
Tässä käytämme distributiivista lakia ja tosiasiaa, että X.X = X ominaisuudesta 9.
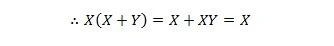
Identiteetti
Kiinteistö 22:
Tämä tarkoittaa, että X + Y -lausekkeessa X:n komplementti Y:n edessä ei muuta lauseketta.
Kiinteistö 23:
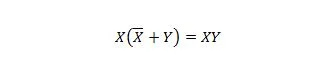
Tämä tarkoittaa, että XY-lausekkeen X ORed -komplementti ja Y suluissa, joka tehdään ensin, ei muuta XY-lauseketta.
DeMorganin laki
Kiinteistö 24:
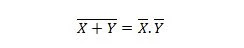
Tämä tarkoittaa, että NOR (NOT OR) -portilla on sama tulos kuin kahden tulon HUOMAUTUS ennen AND-merkintää.
Kiinteistö 25:
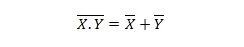
Tämä tarkoittaa, että NAND (NOT AND) -portilla on sama tulos kuin kahden tulon HUOMAUTUS ennen TAI-soittoa.
Toimitetut kuvat ovat 25 ominaisuutta. Ne voidaan todistaa korvaamalla kaikki mahdolliset 1:n ja 0:n arvot kussakin vasemman puolen lausekkeessa, jotta nähdään, saadaanko oikeanpuoleinen lauseke (tai tulos). Todistukset jätetään lukijalle harjoitukseksi.
2.5 Yhdistelmälausekkeiden yksinkertaistaminen
Seuraavat kaksi toimintoa ovat samat:
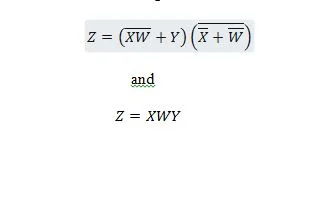
Z on lähtö ja X, W ja Y ovat tulot. Ensimmäinen tarvitsee NAND-portin, TAI-portin, AND-portin, kaksi EI-porttia, TAI-portin ja NOR-portin. Toinen tarvitsee vain kaksi JA porttia. Ensimmäinen on yhtälö, jonka oikealla puolella on yhdistelmälauseke, joka on yksinkertaistettu (pelkistetty) toisen yhtälön yhdeksi oikeanpuoleisen lausekkeen termiksi.
Yksinkertaistaminen tai vähentäminen johtaa pienempään määrään portteja, jotta voidaan toteuttaa sama toiminto kuin piiri. Tällainen pienempi piiri voi olla osa integroitua piiriä (IC) tai olla erillinen piiri tietokoneen emolevyn pinnalla.
Kun funktio (yhtälö) saapuu suunnitteluprosessiin, on tehtävä yksinkertaistamista porttien lukumäärän vähentämiseksi ja päädytään halvempaan piiriin. Yksinkertaistaminen edellyttää yhden tai useamman edellisen 25 Boolen ominaisuuden käyttöä.
Esimerkki 2.51:
Pienennä yhtälö:
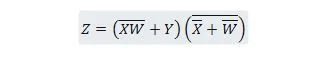
Huomautus: Kaksi vierekkäistä sulkumerkkiä tarkoittaa, että sulut on AND-merkitty (pisteiden väliin ei ole valinnaisesti kirjoitettu).
Ratkaisu:
Ratkaisujen kohdalla kunkin vaiheen perustelu (syy) on annettu askeleen oikealla puolella suluissa. Lukijan tulee lukea jokainen vaihe ja sen perustelut. Lukijan tulee myös viitata edellisiin ominaisuuksiin, kun hän lukee funktion pienennysvaiheita.
Esimerkki 2.52:
Yksinkertaistaa:
2.6 Tuotteiden vähimmäissumma
Seuraavat kaksi toimintoa ovat samat:
Molempien yhtälöiden molempien oikeanpuoleisten lausekkeiden sanotaan olevan Sum of Products (SP) -muodossa. Pikalausekkeen sanotaan olevan Tuotesumma-muodossa, jos siinä ei ole sulkeita. On selvää, että ensimmäinen funktio (yhtälö) tarvitsee enemmän portteja kuin toinen funktio.
Ensimmäinen oikeanpuoleinen lauseke voidaan silti pienentää toisen funktion saamiseksi. Toista oikeanpuoleista ilmaisua ei voida yksinkertaistaa enempää, vaan se ilmaistaan silti tuotteiden summana (termien 'lisäys'). Toista oikeanpuoleista ilmaisua ei voi oikeastaan yksinkertaistaa enempää. Joten sen sanotaan olevan MSP (Minimum Sum of Products) -muodossa.
Esimerkki 2.61:
Tuo seuraava funktio ensin Tuotteiden summa -lomakkeeseen ja sitten Tuotteiden vähimmäissumma -lomakkeeseen.
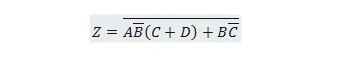
Ratkaisu:
Kun tällaisia ongelmia ratkaistaan, yhtä tai useampaa edellisestä 25 ominaisuudesta on käytettävä tässä ratkaisussa kuvatulla tavalla:
2.6 Tuotteiden vähimmäissumma
Seuraavat kaksi toimintoa ovat samat:
Molempien yhtälöiden molempien oikeanpuoleisten lausekkeiden sanotaan olevan Sum of Products (SP) -muodossa. Pikalausekkeen sanotaan olevan Tuotesumma-muodossa, jos siinä ei ole sulkeita. On selvää, että ensimmäinen funktio (yhtälö) tarvitsee enemmän portteja kuin toinen funktio.
Ensimmäinen oikeanpuoleinen lauseke voidaan silti pienentää toisen funktion saamiseksi. Toista oikeanpuoleista ilmaisua ei voida yksinkertaistaa enempää, vaan se ilmaistaan silti tuotteiden summana (termien 'lisäys'). Toista oikeanpuoleista ilmaisua ei voi oikeastaan yksinkertaistaa enempää. Joten sen sanotaan olevan MSP (Minimum Sum of Products) -muodossa.
Esimerkki 2.61:
Tuo seuraava funktio ensin Tuotteiden summa -lomakkeeseen ja sitten Tuotteiden vähimmäissumma -lomakkeeseen.
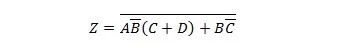
Ratkaisu:
Kun tällaisia ongelmia ratkaistaan, yhtä tai useampaa edellisestä 25 ominaisuudesta on käytettävä tässä ratkaisussa kuvatulla tavalla:
Tämä viimeinen lauseke on tuotteiden summa -muodossa (SP), mutta ei tuotteiden vähimmäissumma -muodossa (MSP). Kysymyksen ensimmäiseen osaan on vastattu. Toisen osan ratkaisu on seuraava:
Tämä viimeinen yksinkertaistettu funktio (yhtälö) on MSP-muodossa, ja sen toteuttamiseen tarvitaan vähemmän portteja kuin vastaava SP-muoto. Muista: SP tarkoittaa tuotteiden summaa, kun taas MSP tarkoittaa tuotteiden vähimmäismäärää.
Esimerkki 2.62:
Seuraavassa piirissä on X-, Y- ja W-tulot ja Z on lähtö. Tuota tuotesumma (SP) -funktio (näennäinen vähimmäistuotesummafunktio) Z:lle. Tuo sitten todellinen pienempi (minimoitu) tuotesumma (MSP). Toteuta sitten MSP-piiri (piirrä MSP-avainnusverkko).
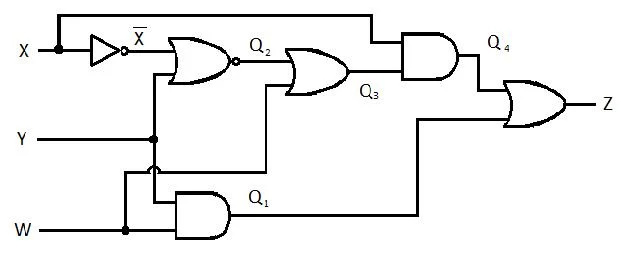
Kuva 2.61 A Gating Circuit
Ratkaisu:
Ennen kuin yksinkertaistaminen alkaa, Z:n lauseke on hankittava X:n, Y:n ja W:n avulla. Katso tämä esimerkkikuva kaaviosta:
Tämä on Z:n ilmaus X:n, Y:n ja W:n suhteen. Tämän jälkeen yksinkertaistaminen näennäiseksi MSP:ksi voi tapahtua. Ilmeinen MSP on SP.
Tämä viimeinen yhtälö (funktio) on SP-muodossa. Se ei pidä paikkaansa Tuotteiden vähimmäismäärä (ei vielä MSP). Joten vähentämistä (minimointia) on jatkettava.
Tämä viimeinen yhtälö (funktio) on todellinen tuotteiden vähimmäissumma (MSP). Ja tuotteiden vähimmäissumma (todellinen minimointi) avainnuspiiri on:
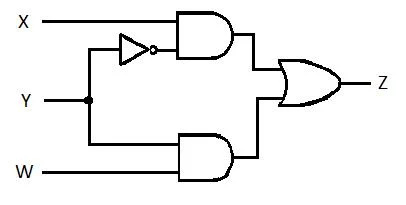
Kuva 2.62 MSP Gating Circuit
Kommentti
Tämän osion analyysistä voidaan nähdä, että ei ole selvää, onko tuotesumma tuotteiden vähimmäissumma vai ei. SP ei ole kovin hyödyllinen. Se on MSP, joka on erittäin hyödyllinen. On varma tapa hankkia MSP; se on käyttää Karnaugh karttaa. Karnaugh Map ei kuulu tämän online-urakurssin piiriin.
2.7 Ongelmat
Lukijaa kehotetaan ratkaisemaan kaikki luvun ongelmat ennen siirtymistä seuraavaan lukuun.
- Tuota AND-, OR- ja NOT-totuustaulukot niitä vastaavien porttien kanssa.
- Kirjoita kymmenen Boolen postulaattia eri kategorioihinsa ja nimeä luokat.
- Kirjoita ilman selitystä Boolen algebran kaksikymmentäkuusi ominaisuutta eri luokkiin ja nimeä luokat.
- Pienennä yhtälö käyttämällä Boolen ominaisuuksia ja lainaamalla käytettyjä luokkia.
- Pienennä yhtälö käyttämällä Boolen ominaisuuksia ja lainaamalla käytettyjä luokkia.
- Käytä Boolen ominaisuuksia ja lainaa käytettyjä luokkia, vähennä seuraava yhtälö – ensin tuotteiden summaksi ja sitten tuotteiden vähimmäissummaksi:
- Käytä Boolen ominaisuuksia ja lainaa käytettyjä luokkia, vähennä seuraava yhtälö – ensin tuotteiden summaksi ja sitten tuotteiden vähimmäissummaksi:
