Luku 3: Binäärilukutoiminnot mikroprosessorissa
3.1 Johdanto
Tietokoneessa aritmeettiset operaatiot tehdään 8-, 16-, 32- tai 64-bittisinä. Luku, kuten 3 binäärimuodossa, on 11. Jos operaatio on tehtävä 8 bitissä, tätä pidetään 00000011; ennen sitä nollalla.
Binääriluvulle, kuten 10000101, merkittävin bitti on äärivasemmalla oleva bitti. Se on tässä tapauksessa 1. Vähiten merkitsevä bitti on oikealla oleva ääribitti, joka on edelleen 1, numerolle. Merkittävin bitti on lyhenne MSB. Vähiten merkitsevä bitti on lyhenne LSB.
Binaariluku on lyhennetty BIT:ksi ja se kirjoitetaan yksinkertaisesti bitiksi. Numerossa 10010011 jokainen yksi tai nolla on bitti. Neljän bitin ryhmää kutsutaan nibbleksi. Kahdeksan bitin ryhmää kutsutaan tavuksi. Tavu koostuu kahdesta nibblestä. Alempi nibble on nibble LSB:lle ja korkeampi nibble on MSB: n nibble.
8 bitin, 16 bitin, 32 bitin tai 64 bitin ryhmää kutsutaan sanaksi, kunhan tämä ryhmä välittää tietoa muutakin kuin vain numeron ilmaisemista. Ryhmää kutsutaan sanaksi esimerkiksi, jos se on tietokoneen matalan tason ohje. On myös 24-bittinen sana, mutta sitä ei käytetä nykyään yleisesti.
Endianness viittaa järjestykseen, jossa tavut muodostavat sanan. Tarkastellaan 24-bittistä sanaa – 100100001111010100100010. Tämä sana koostuu kolmesta tavusta, jotka ovat:
10010000 11110101 00100010
Merkittävin tavu on vasemmanpuoleisin tavu. Kun äärivasemmalla oleva tavu on merkittävin tavu ja äärioikealla oleva tavu vähiten merkitsevä tavu, tätä kutsutaan sanan Big Endian esitykseksi. Little Endian -esitys on päinvastainen.
Tietokoneen muisti on sarja soluja, ja jokaisessa solussa on tavu. Ensimmäinen solu tietokoneen muistissa on tavulle 0, toinen on tavulle 1, kolmas on tavulle 2 ja niin edelleen. Suurella endiannessilla ja edellisen sanan kohdalla merkitsevin tavu tallennetaan tavun 0 soluun, keskimmäinen tavu tavun 1 soluun ja vähiten merkitsevä tavu tavun 2 soluun. Tämä tarkoittaa, että alemmassa muistisolussa on enemmän merkitseviä tavuja.
Edellinen 24-bittinen sana voidaan kirjoittaa käänteisessä tavujärjestyksessä seuraavasti:
00100010 11110101 10010000
Nyt vähiten merkitsevä tavu on äärivasemmalla ja merkittävin tavu äärioikealla. Kun äärivasemmalla oleva tavu on vähiten merkitsevä tavu ja äärioikealla oleva tavu on merkittävin tavu, se on sanan Little Endian -esitys. Vähiten endiannessa ja edellisen sanan osalta vähiten merkitsevä tavu tallennetaan tavun 0 soluun, keskimmäinen tavu tavun 1 soluun ja merkittävin tavu tavun 2 soluun. Tämä tarkoittaa, että alemmassa muistisolussa on vähemmän merkitsevää tavua.
Endianssia ei käytetä tavun biteille. Sitä ei myöskään käytetä tavun nibbleihin. Sitä käytetään vain tavujärjestykseen.
Numerorivi
Luku ilman etumerkkiä on positiivinen luku. Positiiviset luvut ovat lukuja nollasta ylöspäin. Myös negatiivisia lukuja on olemassa. Positiiviset ja negatiiviset luvut voidaan esittää lukurivillä. Seuraava numerorivi näyttää positiiviset ja negatiiviset kokonaisluvut (kokonaisluvut) lähellä nollaa:
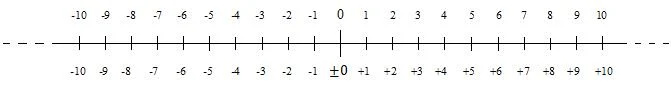
Negatiiviset luvut pienenevät nollasta alaspäin (vasemmalle). Monissa tilanteissa nollaa pidetään positiivisena. Sitä pidetään kuitenkin joissakin tilanteissa negatiivisena. Siksi kaaviossa on plus- ja miinusmerkki nollan edessä, alemmassa numeroinnissa. Kun luku on positiivinen, sen etumerkki voidaan jättää pois; tämä pätee kaavion ylempään numerointiin. Miinusmerkkiä negatiivisen luvun edessä ei koskaan jätetä pois.
3.2 Binäärilukujen lisääminen
Lisäksi:
A + B = S
A:ta kutsutaan lisäykseksi, B:tä kutsutaan summaksi ja S:ksi summaksi.
Harkitse seuraavaa kahden positiivisen luvun lisäystä kahdessa perusluvussa:

Kahdessa kantaluvussa ainoat mahdolliset numerot ovat 0 ja 1. Summaisuus kannassa 2 on samanlainen kuin yhteenlasku kantakannassa 10, mutta kaksi kakkoskannassa on yksi nolla (10). Kun sarakkeen kahden bitin summa on 10, kirjoitetaan 0 ja 1 siirretään välittömään vasempaan sarakkeeseen; lisätään kahden siellä olevan bitin summaan. Kun kokonaissumma on kolme, se tarkoittaa 11 kakkosarvossa. Oikea 1 in 11 kirjoitetaan ja vasen 1 lisätään välittömän vasemman sarakkeen bittien summaan. Kummassakin tapauksessa vasemmalle siirrettyä 1:tä kutsutaan kantamiseksi.
Lukeessa edellistä summaustaulukkoa oikealta, toisessa sarakkeessa (oikealta) on siirto, joka johtuu 1+1 = 10. Kolmannessa sarakkeessa on siirto, joka johtuu 1+1+ siirrosta 1 = 11. Neljännessä sarakkeessa on siirto, joka johtuu 0+1+ siirrosta 1 = 10. Viidennessä sarakkeessa ei ole siirtoa, koska summa on 0+0+ siirto 1 = 1. loput sarakkeet eivät sisällä kuljetusta.
Sarakkeiden laskenta alkaa oikeasta päästä. 16-bittisellä lisäyksellä voi tapahtua siirto kahdeksannesta sarakkeesta yhdeksänteen sarakkeeseen (siirretään vasemmalle). Seuraava taulukko havainnollistaa tätä:

Aritmeettiset ja logiikkatoiminnot tapahtuvat tietokoneen emolevyn mikroprosessorissa.
8-bittisessä sanatietokoneessa siirto ei voi siirtyä automaattisesti kahdeksannnesta bitistä yhdeksänteen bittiin laitteiston toimesta. Jotta tällaiseen tietokoneeseen voidaan lisätä kaksi 16-bittistä ryhmää, lisäys on tehtävä kahdesti kahdeksaan-kahdeksaan bittipariin. Kanto siirretään ja suoritetaan ohjelmistolla (ohjelmointi).
Kahden luvun lisäämiseksi luvut voidaan muuntaa ensin niiden kahden komplementtimuotoon (katso alla) ennen lisäämistä.
3.3 Kahden komplementti ja sen vähennys binääriluvuista
Tietokoneen emolevyllä on muisti ja siellä on mikroprosessori ja muut piirit. Muisti on sarja kahdeksan bittisiä soluja. Tavua kohden jokainen bitti menee soluun. Mikroprosessorissa on muutamia muistityyppisiä paikkoja. Näitä muistityyppisiä paikkoja kutsutaan rekistereiksi. Joten tietokoneessa tavuryhmiä voidaan tallentaa väliaikaisesti muistiin tai mikroprosessorin rekistereihin.
Missä tahansa näistä varastoista jokainen solu voi ottaa joko 1:n tai 0:n, eikä mitään muuta. Elämässä on positiivisia ja negatiivisia lukuja. Positiivinen luku alkaa plusmerkillä (+) ja negatiivinen luku alkaa negatiivisella merkillä (-). Kun merkki jätetään pois, lukua pidetään positiivisena lukuna.
Tämän ongelman ratkaisemiseksi, joka liittyy luvun etumerkin osoittamiseen tietokoneessa, kokonaisluvut tallennetaan alueille. Kokonaisluvut ovat kokonaislukuja. Jos mahdollisten lukujen alueen tallentamiseen käytetään kahdeksaa bittiä, etumerkkibittinä käytetään vasemmanpuoleista bittiä. Jos luku alkaa nollalla, luku on positiivinen luku. Jos se alkaa luvulla 1, luku on negatiivinen luku. Jos mahdollisten lukujen alueen tallentamiseen käytetään kuuttatoista bittiä, etumerkkibittinä käytetään vasemmanpuoleista bittiä. Jos luku alkaa nollalla, t luku on positiivinen luku. Jos se alkaa luvulla 1, luku on negatiivinen luku. Tässä muodossa olevia numeroita kutsutaan etumerkillisiksi numeroiksi.
Käytännössä etumerkityt numerot voivat olla 8-, 16-, 32- ja 64-bittisiä. Mitä laajempaa bittimäärää käytetään, sitä suurempi on mahdollisten numeroiden valikoima, joka voidaan tallentaa.
Kahden täydentävät kokonaisluvut
Kahden komplementin kanssa positiiviset luvut ovat normaaleja laskentalukuja, paitsi että vasemmanpuoleisin numero on 0. Saadaksesi vastaava negatiivinen luku mille tahansa positiiviselle luvulle, käännä luvun jokainen bitti ja lisää tulokseen 1. Numeron 0 invertti tai komplementti on 1. 1:n käänteis tai komplementti on 0. Seuraavissa taulukoissa on joidenkin kahden komplementtinumerot omissa rajoissaan:
| Taulukko 3.31 Two's Täydentävät kokonaisluvut kahdessa bitissä |
|
|---|---|
| Binääri | Desimaali |
| 01 | +1 |
| 00 | +0 |
| yksitoista | -1 |
| 10 | -2 |
Positiiviset binääriluvut ovat 00 ja 01 (eli nolla ja yksi). Vasemmalla olevassa bitissä nolla osoittaa, että ne ovat positiivisia lukuja. 00 on jonkin verran alueen puolivälissä. Jotta saadaan -1, luvun 01 invertti on 10. Kun tähän lisätään 1 (äärioikealla), saadaan 11.
Koska käytetään kahta bittiä, vain yksi bitti jää edustamaan numeroita alueella, joka koostuu numeroista +1, +0 ja -1, jotka vastaavat numeroita 01, 00 ja 11. Ensimmäinen bitti ilmaisee etumerkin. Sattuu niin, että 10 +2:lle ei ole näiden kolmen binääriluvun joukossa. 10 alkaa luvulla 1, mikä tarkoittaa, että sen on oltava negatiivinen luku kahden komplementissa. Joten 10 sisältyy alueeseen, mikä tarkoittaa -2.
Kun kahden bitin komplementissa on kaksi bittiä, kaikkien kokonaislukujen (positiivisten ja negatiivisten) lukumäärä, jotka voidaan esittää, on 2 2 = 4 eikä 2 2 -1 = 3. Vivahde johtuu viimeisen negatiivisen luvun sisällyttämisestä, joka on luvun 2 negatiivinen numeron kanssa – 1. Tässä tapauksessa -2 2-1 = -2 1 = -2. Kahden komplementtiluvun alueella ei ole +2:ta 2 bitissä.
| Taulukko 3.32 Kahden täydentävät kokonaisluvut neljässä bitissä |
|
|---|---|
| Binääri | Desimaali |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
Positiiviset binääriluvut ovat 0000 - 0111 (eli nollasta seitsemään). Vasemmalla olevassa bitissä nolla osoittaa, että ne ovat positiivisia lukuja. 0000 on jonkin verran alueen puolivälissä. Jotta saadaan -1, luvun 0001 invertti on 1110. Kun tähän lisätään 1 (äärioikealla), saadaan 1111. Jotta saadaan -2, luvun 0010 invertti on 1101. Kun tähän lisätään 1 ( äärioikealta) antaa 1110. Muut negatiiviset binääriluvut, kuten -3 - -7, määritetään samalla tavalla.
Koska käytössä on neljä bittiä, kolme bittiä jää edustamaan alueen numeroita, jotka ovat +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 ja -7, jotka vastaavat numeroita 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, 1010 ja 1010.
-8, joka vastaa lukua 1000, on käsiteltävä erikseen. Ensimmäinen bitti kaikille näille numeroille osoittaa 0:n etumerkkiä positiivisille luvuille ja 1:n negatiivisille luvuille. Sattuu niin, että 1000 ei ole näiden neljäntoista binääriluvun joukossa. 1000 alkaa luvulla 1, mikä tarkoittaa, että sen on oltava negatiivinen luku kahden komplementin osalta. Joten 1000 sisältyy valikoimaan, mikä tarkoittaa -8.
Neljällä bitillä kahden komplementissa kaikkien kokonaislukujen (positiivisten ja negatiivisten) lukumäärä, jotka voidaan esittää, on 2 4 = 16 eikä 2 4 – 1 = 15. Vivahde johtuu viimeisen negatiivisen luvun sisällyttämisestä, joka on luvun 2 negatiivinen numeroLeveys – 1. Tässä tapauksessa -2 4 -1 = -2 3 = -8. Numeroalueella ei ole +8.
Aiempaa analyysiä kahdelle, neljälle ja leveämmille biteille kahden komplementissa voidaan soveltaa 8 bitin, 16 bitin, 32 bitin ja 64 bitin leveisiin binäärilukuihin.
Kahden komplementti uhraa ensimmäisen (vasemmanpuoleisen) bitin 0:n etumerkille positiiviselle luvulle ja 1:lle negatiiviselle luvulle. 'n'-bitin levyiselle bittiryhmälle on 2 n yhteensä positiiviset plus negatiiviset luvut. Se olisi 2 n -1, ellei mukana olisi onnekas viimeinen (pienin) negatiivinen luku. Suurin positiivinen luku on +2 n-1 -1 ja pienin negatiivinen luku on -2 n-1 -1. Se olisi -2 n-1 -1, jos ei olisi onnekas -2 n-1 mukana.
Lukujen vähentäminen kahden komplementissa
Vähennyksessä:
A – B = D
A:ta kutsutaan minuuttiksi, B:tä aliosaksi ja D:ksi erotukseksi.
Jos haluat vähentää yhden positiivisen binääriluvun toisesta positiivisesta binääriluvusta, minuutti kirjoitetaan kahden komplementin mukaan ja aliosa muunnetaan negatiivisen kahden komplementin arvoksi. Joten matemaattisesta lauseesta tulee:
A+ – B = D
Toisin sanoen kahden komplementin vähennyslaskussa aliosa muunnetaan negatiiviseksi luvuksi ja lisätään sitten minuuttiin.
Esimerkki 3.31:
Arvioi seuraava desimaalilauseke kahden komplementissa käyttämällä neljää bittiä:
6-4
Ratkaisu:
Binääriluku 6:lle on 110. 4-bittisessä kahden komplementissa se on 0110. Binääriluku +4:ssä on 100. 4-bittisessä kahden komplementissa se on 0100. 0100, joka on muutettava negatiiviseksi 4 kahdessa komplementti seuraavasti: 0100:n komplementti tai inversio on 1011. Kun tähän lisätään 1 oikeasta päästä, kuten teimme lisäksi, saadaan 1100. Eli desimaalilauseke on:
6–4, josta tulee:
0110 - 0100 eli
0110 +(– 0100) = 0110 + 1100 tehty kuten edellisessä lisäysosassa seuraavasti:

Huomautus: 0110 +(– 0100) on sama kuin 6 + – 4
Kahden komplementin vähennyslaskulla kaikki siirto viimeisen sarakkeen jälkeen vasemmalle lasketaan pois. Kun vähennetään desimaaliluvulla, matemaattinen lause on:
6-4 = 2
Kun tehdään sama asia kahden komplementissa, vastaus on 0010, joka on +2 kahden komplementin binäärilaskennassa. Edellinen vähennyslasku vähentää pienemmän luvun suuremmasta luvusta. Seuraavassa esimerkissä suurempi luku vähennetään pienemmästä numerosta. Taulukosta 3.32 voidaan katsoa, onko 0010 todella kahden komplementti, joka vastaa +2:ta.
Esimerkki 3.32:
Arvioi seuraava desimaalilauseke kahden komplementin neljällä bitillä:
4-6
Ratkaisu:
Binääriluku 4:lle on 100. 4-bittisessä kahden komplementissa se on 0100. Binääriluku +6:ssa on 110. 4-bittisessä kahden komplementissa se on 0110. 0110 on muutettava negatiiviseksi 6:ksi kahden komplementissa seuraavasti: 0110:n komplementti tai inversio on 1001. Kun tähän lisätään 1 oikeasta päästä, kuten teimme edellisessä lisäyksessä, saadaan 1010. Eli desimaalilauseke on:
4–6, josta tulee:
0100 - 0110 eli
0100 +(– 0110) = 0100 + 1010 tehty kuten edellisessä lisäysosassa seuraavasti:

Huomautus: 4+ – 6 on sama kuin 0100 +(– 0110).
Kahden komplementin vähennyslaskulla kaikki siirto viimeisen sarakkeen jälkeen vasemmalle lasketaan pois. Kun vähennetään desimaaliluvulla, matemaattinen lause on:
4-6 = -2
Kun tehdään sama asia kahden komplementissa, vastaus on 1110, joka on -2 kahden komplementin binäärilaskennassa. Taulukosta 3.32 voidaan katsoa, onko 1110 todella kahden komplementti, joka vastaa -2:ta.
3.4 Binäärilukujen kertominen
Lausunnossa:
A x B = P
A:ta kutsutaan kertojaksi, B:tä kertojaksi ja P:ksi tuloksi. A x B -lauseke tarkoittaa A:n, B:n yhteenlaskua, kun A ja B ovat kokonaislukuja (kokolukuja).
Kertominen binäärimuodossa on sama kuin kertolasku desimaaliluvulla. Sen sijaan, että se tekisi sen desimaalimuodossa, se tehdään binäärimuodossa. Desimaalilausekkeen 42 x 10 kertolasku tehdään binäärimuodossa seuraavasti, missä 42 10 = 101010 2 ja 10 10 = 1010 2 :
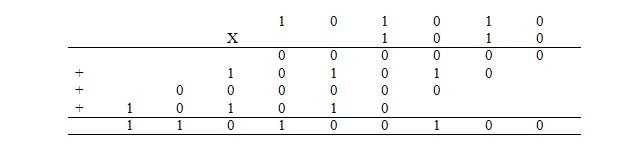
Lisättyjä neljää numeroa kutsutaan osittaisiksi tuotteiksi. Vastaus on tuote. Osittaisten tuotteiden lisääminen tapahtuu samalla tavalla kuin aiemmin selitettiin.
Kertominen voidaan nähdä myös seuraavasti: Tässä peruskaksikertolaskussa, jos kertojan bitti (numero) on 1, sen osittaistulon vähiten merkitsevä bitti on kertojan vähiten merkitsevä bitti, joka kirjoitetaan uudelleen suoraan sen alle; ja kertojan loput bitit toistetaan vasemmalle. Tässä peruskaksikertolaskussa, jos kertojan bitti (numero) on 0, sen osatulo koostuu noloista, joiden vähiten merkitsevä bitti on 0 suoraan sen alla. Kaikkien nollien määrä on kertojan bittien määrä.
3.5 Binäärilukujen jako
Lausunnossa:
A ÷ B = Q
A:ta kutsutaan osinkoksi, B:tä jakajaksi ja P:tä osamääräksi. Osamäärään voi liittyä jäännös. A ÷ B -lauseke tarkoittaa, kuinka monta kertaa B voidaan lisätä antamaan A tai olla lähellä sitä siten, että jäännös on 0 tai pienempi kuin B.
Jako voidaan tehdä monella tapaa. Tässä esitetty jako on restaurointijako.
Divisioonan palauttaminen
Tämä on kouluissa opittu pitkä jakomenetelmä. Jos 237 jaetaan 6:lla, vastaus on 39 jäännös 3. 237 10 pohjassa 2 on 11101101 2 ja 6 10 pohjassa 2 on 110 2 . 39 10 pohjassa 2 on 100111 2 ja 3 10 pohjassa 2 on 11 2 .
Joten, 11101101 2 jaettuna 110:llä 2 antaa 100111 2 loput 11 2 kahdessa pohjassa. Palautusmenetelmällä binääriluvut ovat tavallisia lukuja, eivätkä ne välttämättä ole kahden komplementissa. Seuraava rakenne jakaa 11101101 2 110 mennessä 2 antaa 100111 2 loput 11 2 :

Vähennys tehdään tavallisesti eikä käyttämällä kahden komplementtia. Koska tämä on perusta kaksi, laina on kaksi eikä kymmenen. Osaosingot ovat 10, 101, 1011, 1010 ja 1001. 11 on loppuosa. Koska jakajassa on kolme numeroa, jako tehdään periaatteessa kolmen numeron ryhmissä annetusta osingosta. Osamäärä on kokonaisluku (kokonaisluku), ja se on 100111 tälle tehtävälle. Osamäärä ja jäännöstulos ovat odotetusti.
3.6 Aritmeettiset operaatiot ohjelmiston ja laitteiston kanssa
Tietokoneen emolevyssä on kello. Kellon tikityksiä kutsutaan pulsseiksi. Jokaisella kellopulssilla tehdään yksi tai useampi päätös emolevyn eri kohdissa; ja se liittyy ohjelmointiin (ohjelmistoon).
Mikroprosessorin sisällä on kahdenlaisia piirejä, joita kutsutaan: yhdistelmälogiikkapiireiksi ja peräkkäisiksi logiikkapiireiksi. On olemassa toisenlainen piiri, jota kutsutaan multiplekseriksi. Yhteen-, kerto- ja jakolasku voidaan suorittaa yhden kellovälin sisällä käyttämällä yhdistelmälogiikkaa (piiriä). Ohjelmoinnin aikana (ohjelmisto) tekee päätöksen jokaisella kellopulssilla käyttämällä peräkkäisiä logiikkapiirejä ja multipleksereitä.
Kun vähennys tehdään kahden komplementin avulla, vähintään kaksi kellopulssia tarvitaan. Ensimmäisellä kellopulssilla multiplekseri kanavoi aliosan EI-porttien joukoksi (yksi NOT-portti per numero). Toisella kellopulssilla yhdistelmälogiikka lisää 1:n NOT-porttien lähtöön ja jatkaa tuloksena olevan aliosan ja minuutin lisäämistä. Kaikki tämä lisäys voi tapahtua yhden kellovälin sisällä.
Yhteen-, kerto- ja jakolasku voi silti olla alhaalla ohjelmoimalla totuustaulukoita käyttäen. Sitä ei kuitenkaan käsitellä tässä online-urakurssissa.
3.7 Logiikkatoiminnot mikroprosessorissa
AND, OR, XOR ja Invert
JA
Seuraava taulukko havainnollistaa Bitwise AND. Tämä tarkoittaa, että kahdelle eri binääriluvulle vastaavat bitit AND-edetaan AND-totuustaulukon perusteella:
Siirtyminen vasemmalta oikealle, 1 JA 1 = 1; 0 JA 1 = 0; 0 JA 0 = 0; 1 JA 0 = 0; ja niin edelleen JA Totuustaulukon mukaisesti.
TAI
Seuraava taulukko havainnollistaa bittikohtaista TAI:ta. Tämä tarkoittaa, että kahdelle eri binääriluvulle vastaavat bitit TAI-arvotaan TAI-totuustaulukon perusteella:

Siirtyminen vasemmalta oikealle, 1 TAI 1 = 1; 0 TAI 1 = 1; 0 TAI 0 = 0; 1 TAI 0 = 1; ja niin edelleen OR Truth Table -taulukon mukaisesti.
VAPAA
Seuraava taulukko havainnollistaa Bitwise-exclusive-OR-toimintoa. Tämä tarkoittaa, että kahdelle eri binääriluvulle vastaavat bitit XOR-korjataan XOR-totuustaulukon perusteella:

Siirtyminen vasemmalta oikealle, 1 XOR 1 = 0; 0 XOR 1 = 1; 0 XOR 0 = 0; 1 XOR 0 = 1; ja niin edelleen XOR Truth Table -taulukon mukaisesti.
Käänteinen (EI)
Seuraava taulukko havainnollistaa Bitwise NOT (käänteinen). Tämä tarkoittaa, että yhdellä binääriluvulla tällä kertaa jokainen bitti käännetään NOT Truth Table -taulukon perusteella:

Liikkuu vasemmalta oikealle, EI 1 = 0; EI 0 = 1; EI 0 = 1; EI 1 = 0; ja niin edelleen NOT Truth Table -taulukon mukaisesti.
Vaihto oikealle tai vasemmalle
Vaihto oikealle
Seuraavaa binaarilukua siirretään 3 bittikohtaa oikealle, ja nollat lisätään vasemmalla olevaan vapautettuun bittipaikkaan:

Siirto voidaan tehdä yhdelle, kahdelle, kolmelle, neljälle jne. paikalle.
Vaihto vasemmalle
Seuraavaa binaarilukua siirretään 3 bittiä vasemmalle, ja nollat lisätään oikealla oleviin vapautettuihin bittipaikkoihin:

Siirto voidaan tehdä yhdelle, kahdelle, kolmelle, neljälle jne. paikalle.
Pyöriminen oikealle tai vasemmalle
Pyöriminen on samanlaista kuin vaihtaminen. Se tehdään pala kerrallaan. Oikealle käännettäessä oikeasta päästä lähtevät terät eivät putoa kuten vaihdossa; ne korvaavat vasemmalla olevat tyhjät bitit yksitellen. Vasemmalle käännettäessä vasemmasta päästä lähtevät terät eivät putoa kuten vaihdossa; ne korvaavat oikealta vapautuneet bitit yksitellen.
Kierrä oikealle
Seuraavaa binaarilukua kierretään 3 bittiä oikealle:

Pyörimistä voidaan tehdä yhdelle, kahdelle, kolmelle, neljälle jne. paikalle.
Rorate vasemmalle
Seuraavaa binaarilukua kierretään 3 bittiä vasemmalle:

Pyörimistä voidaan tehdä yhdelle, kahdelle, kolmelle, neljälle jne. paikalle.
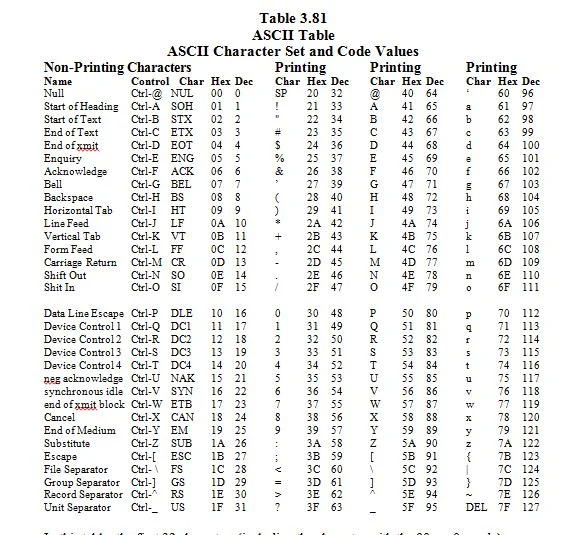
3.8 ASCII-merkkijoukko ja sen koodiarvot
ASCII tarkoittaa 'American (U.S.A) Standard Code for Information Interchange'. Kuvittele näppäimistö, jossa on 96 näppäintä. Tämä on ihanteellinen näppäimistö, jossa isot kirjaimet ovat erilaisia kuin pienet kirjaimet. Jokainen toinen näppäin edustaa merkkiä, joka löytyy englanninkielisestä (USA) näppäimistöstä. Merkit ja koodit (merkkien vastaavat numerot) on lueteltu seuraavassa:
Tässä taulukossa ensimmäiset 32 merkkiä (mukaan lukien merkki, jossa on 00 16 = 0 10 koodi) ovat ei-tulostuvia merkkejä. Ne ovat ohjaushahmoja. Niitä ei näy näytöllä (monitorissa), jossa kaikki on tasa-arvoista. Niillä on vain vaikutuksia. Keskustellaan siitä lisää myöhemmin.
Loput merkit ovat tulostusmerkkejä; ne näkyvät näytöllä. ASCII-merkkejä on 128. 2 7 = 128. 1,111,111 2 = 127 10 . 7 in 2 7 tarkoittaa 7 bittiä.
Nyt 1111111 2 + 1 2 on sama kuin:
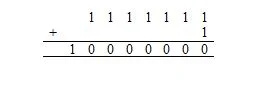
Tässä 10 000 000 2 = 128 10 . Niitä on 128 10 merkit edellisessä ASCII-merkkiluettelossa (taulukossa). Tämä sisältää nollamerkin, jonka koodi kantaluvussa kuusitoista (heksadesimaali) on 00, mikä vastaa 0:aa kymmenessä kannassa.
Koska merkkejä on yhteensä 128, 128 miinus 32 ei-tulostuvaa merkkiä antaa 96 tulostettavaa merkkiä. Tässä osiossa oletetaan, että on olemassa ihanteellinen näppäimistö, jossa on 96 merkkiä, jotka ovat tulostettavia merkkejä. Tässä ihanteellisessa näppäimistössä englannin isojen kirjainten näppäimet eroavat englannin pienten kirjainten näppäimistä.
Jokainen näppäimistön merkki on esitetty kahdella 7-bitin perusluvulla, joita ei näytetä luettelossa. Esimerkiksi isoa kirjainta 'N' edustaa seitsemän bittiä 1001110 kannassa 2. Muuntaaksesi 1001110 2 kantaan 16, edeltää sitä 0:lla ja ryhmittele tulos nelibittisiin alaryhmiin seuraavasti:
| 0100 | 1110 | 2 = | 4 | E | 16
Se on 01001110 2 = 4E 16 . Muuntaa 4E 16 kymmeneen kantaan, toimi seuraavasti:
4 x (16) 1 + E x (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
Luettelon (taulukon) N:n oikealla puolella on heksadesimaaliluku 4E ja desimaaliluku 78.
Toisena esimerkkinä '['-merkkiä edustavat seitsemän bittiä 1011011 kannassa 2. Muuntaaksesi 1011011 2 kantaan 16, edeltää sitä 0:lla ja ryhmittele tulos nelibittisiin alaryhmiin seuraavasti:
| 0101 | 1011 | 2 = | 5 | B | 16
Se on 01011011 2 = 5B 16 . Muunna 5B16 peruskymmeneksi seuraavasti:
5 x (16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
Luettelon (taulukon) '[' oikealla puolella on heksadesimaaliluku 5B ja desimaaliluku 91.
Toisena esimerkkinä desimaaliluvun '5' merkkiä edustavat seitsemän bittiä 0110101 kannassa 2, ja ei 0000101 kannassa 2. Muuntaa 0110101 2 kantaan 16, edeltää sitä 0:lla ja ryhmittele tulos nelibittisiin alaryhmiin seuraavasti:
| 0011 | 0101 | 2 = | 5 | B | 16
Se on 00110101 2 = 35 16 . Jos haluat muuntaa 3516 peruskymmeneksi, toimi seuraavasti:
3 x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
Luettelon (taulukon) '5':n oikealla puolella on heksadesimaaliluku 35 ja desimaaliluku 53.
Koska tietokone toimii tavuissa, kun ihanteellisen näppäimistön näppäintä painetaan, mikroprosessorille (emolevylle) lähetetään kahdeksan bittiä. Ihanteellinen näppäimistö on oheislaite, joka on erotettu tietokoneen järjestelmäyksiköstä (perusyksikkö). Siinä on elektroninen piiri (IC), joka luo seitsemän bittiä ja edeltää sen nollalla ennen kuin se lähettää sen kaapelin kautta järjestelmäyksikön emolevylle. Emolevyn tuloportista (tulopiiristä) se menee mikroprosessoriin, joka on myös emolevyssä. Mikroprosessorista se menee muistiin, joka on myös asennettu emolevylle.
Joten kun ihanteellisen näppäimistön 'N'-näppäintä painetaan, mikroprosessoriin viedään kahdeksan bittiä 01001110. Mikroprosessorista ne viedään muistiin, jossa ne jäävät muistipaikkaan tavuna. Ohjelmoijan tulee pitää mielessä, että numeron 01001110 kahdeksan bittiä 2 on sama kuin 4E 16 joka on sama kuin 78 10 .
Kun ihanteellisen näppäimistön '['-näppäintä painetaan, mikroprosessoriin siirretään kahdeksan bittiä 01011011. Mikroprosessorista ne viedään muistiin, jossa ne jäävät muistipaikkaan tavuna. Ohjelmoijan tulee pitää mielessä, että numeron 01011011 kahdeksan bittiä 2 on sama kuin 5B 16 joka on sama kuin 91 10 .
Kun ihanteellisen näppäimistön '5'-näppäintä painetaan merkkinä eikä desimaalilukuna, mikroprosessoriin viedään kahdeksan bittiä 00110101. Mikroprosessorista ne viedään muistiin, jossa ne jäävät muistipaikkaan tavuna. Ohjelmoijan tulee pitää mielessä, että numeron 00110101 kahdeksan bittiä 2 on sama kuin 35 16 joka on sama kuin 5310 10 .
Joskus ohjelma on käynnissä ja odottaa, että desimaaliluku 5 syötetään tietokoneeseen. Tässä tilanteessa, jos ihanteellisen näppäimistön “5”-näppäintä painetaan, mikroprosessoriin viedään silti kahdeksanbittinen koodi 00110101. Koska tarvitaan desimaaliluku 5, ei 5-merkkiä, muistista tuleva koodinpätkä (lyhytohjelma) käyttää mikroprosessoria muuntaakseen kakkosluvun 00110101 merkkikoodin kahden komplementtinumeroksi 00000101. 2 ennen sen lähettämistä muistipaikkaan kahden komplementin tavuna. Ohjelmoijan on pidettävä mielessä, että 00000101 tarkoittaa 5 10 kanta 2, ja se eroaa koodinumeroista 00110101 2 , 35 16 ja 53 10 mikä tarkoittaa '5'-merkkiä. Näiden kahden komplementtiluvun 00000101 näyttämiseksi muistissa toisen lyhyen ohjelman on muutettava 00000101 muistista numeroksi 00110101. Se on 00110101, joka on sama kuin 35. 16 joka on sama kuin 53 10 joka näkyy näytössä (tai tulostin tulostaa paperille).
3.9 Liukulukumuoto
Luku ilman desimaaliosaa on kokonaisluku. Luku 36 on kokonaisluku. 36,375 ei ole kokonaisluku. Se on desimaaliluku, jossa on desimaaliosa. 0,375:n desimaaliosa on murtoluku, joka on pienempi kuin 1.
36.375 tulkitaan desimaalimuodossa seuraavasti:
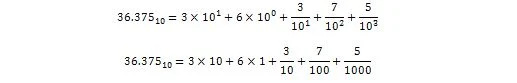
Nyt:
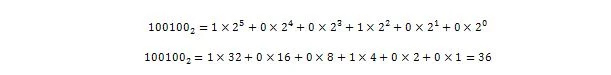
Eli 100100 2 = 3610, joka on luvun 36,375 kokonaislukuosa 10 .
Nyt:
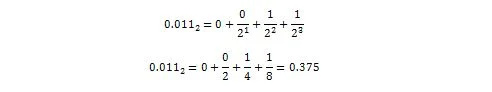
Eli 0,011 2 = 0,375 10 joka on 36.375:n desimaalilukuosa 10 .
∴ 36 375 10 = 100100.011 2
Laita se toisin:
100100.011 2 = 36 375 10
Numerot esitetään tietokoneessa kannassa 2 eikä kannassa 10, kun kaikki on yhtä suuria. Koska mikroprosessorin rekisterissä tai muistissa oleva solu voi olla vain 1 tai 0, desimaalipilkun tallentamiseen ei ole tilaa. Tämä aiheuttaa ongelmia. Resoluutiona on IEEE-754 yksitarkkuus 32-bittinen liukulukuesitys ja IEEE-754 kaksinkertainen tarkkuus 64-bittinen liukulukuesitys.
32-bittinen liukulukumuoto
Numero 100100.0112 voidaan ilmaista seuraavasti:
100100.011 2 = 1,00100011 2 x 2 +5
=-symbolin oikeaa puolta kutsutaan matematiikassa luvun 100100.011 vasemman puolen kahdeksi perusmuodoksi. 2 .
Nyt 00100011 / 1,00100011 2 =-symbolin oikealla puolella ilman edeltävää '1'. ja ilman kantaa 2, kutsutaan eksplisiittiseksi merkitseväksi. Tässä tapauksessa binääripiste siirretään viisi paikkaa vasemmalle, jotta se saa '1'. Älä sekoita desimaalipilkkua ja binääripistettä. Binääripiste on kantaluku 2, kun taas desimaalipiste on kantaluku 10. '1'. ja sen jälkeen 00100011 =-symbolin oikealla puolella, ilman kantaa 2, muodostaa todellisen merkityksen. Kuitenkin 1.00100011 kutsutaan implisiittiseksi merkitseväksi.
Merkinnän jälkeen oikealla on 'x 2 +5 ' ilmaisu. Tällä lausekkeella +5:tä kutsutaan eksponenttiksi. Plus-merkki tarkoittaa, että binääripistettä on siirrettävä viisi paikkaa eteenpäin, jotta se olisi normaalissa alkuperäisessä paikassaan ja 2 on numeroinnin perusta. Edellinen yhtälö voidaan kirjoittaa käänteisesti seuraavasti:
1,00100011 2 x 2 +5 = 100100.011 2
32-bittisessä liukulukuesityksessä se on '1.00100011 2 x 2 +5 ', jota käytetään, eikä vain '100100.011 2 ”. Tukikohdan numeroa 2 ei ole tallennettu. 32-bittinen liukulukuesitys kohteelle '1.00100011 2 x 2 +5 ”-numero, joka on yhtä suuri kuin 36.375 10 = 100100.011 2 , näkyy seuraavassa taulukossa:

On olemassa 32-bittisiä paikkoja, jotka on numeroitu oikeasta päästä alkaen 0:sta. Ensimmäinen bitti vasemmassa päässä on etumerkkibitti. Jos luku on positiivinen, tämä bitti on 0. Jos luku on negatiivinen, tämä bitti on 1 (-1 koostuu kahdesta merkistä eikä sitä voi laittaa yhteen soluun). 1.00100011 2 x 2 +5 joka on yhtä suuri kuin 36,375 10 joka on myös yhtä kuin 100100.011 2 on positiivinen luku. Ensimmäinen bitti on siis 0.
Eksponentille on kahdeksan bittipaikkaa alkaen paikasta 30 kohtaan 23, mukaan lukien. Sinne kirjoitettu eksponentti on kuitenkin 10000100 2 joka on yhtä suuri kuin 132 10 . Kiinnostuksen luvun eksponentti on itse asiassa +5 kahdesta. Mitä tapahtuu?
Nyt 32-bittisessä muodossa 0:n eksponentti kirjoitetaan muodossa 01111111 2 joka on yhtä suuri kuin 127 10 . +5 10 on +101 2 . Joten saapuessaan 10000100 2 taulukon eksponenttiosassa 101 2 lisättiin numeroon 01111111 2 , vastaavasti. Se tarkoittaa, että 5 lisättiin 127:ään, jolloin saatiin 132 10 .
Merkittävä, ilman '1.', vei sijoitukset 22 alas 15:een, mukaan lukien. Huomaa, että 1 luvusta 1. ei ole ilmoitettu 32-bittisessä merkkijonossa. Sitä ei koskaan mainita – hyväksy se. Loput solut kohtaan 0 on täytetty nollilla.
Jos todellinen eksponentti on -5, 5 vähennetään luvusta 127 10 saada 122 10 . Tämä vastaa 101:n vähentämistä 2 alkaen 01111111 2 saada numero 01111010 2 .
Kaikessa edellisessä kuvassa numero +1, joka on yhtä suuri kuin 1,0 x 2 0 = 1,0 x 1 = 1,0 esitetään seuraavasti:

Huomaa, että '1.' 1,0 x 2 0 ei ole ilmoitettu muodossa. Sitä ei ole koskaan ilmoitettu. Seuraava sekaluku, joka menee positiivisesti arvon 1,0 jälkeen, on:

Huomaa 1 oikeassa päässä. Tämä esitys on numero:

Ero 1.0000001192092896 ja 1.0 välillä on:
1,0000001192092896 – 1,0 = 0,0000001192092896
Desimaaliluvuilla varustetut luvut ovat sekamurtolukuja. Ei kaikki murtoluvut 1:n välillä 10 ja 2 10 voidaan esittää tietokoneessa. Voidaan olettaa, että pienin murto-ero peräkkäisten sekalukujen välillä 32-bittisessä liukulukumuodossa on 0,0000001192092896. Odota, että kaksinkertaisen tarkkuuden väli on pienempi. Katso seuraavaa kuvaa.
Lukua edustava 0.0 ei noudata edellisiä argumentteja. 0.0:n esitys ilmoitetaan ja se on opittava sellaisenaan. Arvon 0,0 esittämiseksi kaikki merkitsevän ja arvosanan solut ovat nollia ja kaikki eksponentin solut ovat myös nollia. Etumerkkibitti voi olla 0 tai 1. Valitettavasti tästä syntyy positiivinen 0 ja negatiivinen 0 seuraavasti:

Tosielämässä on vain yksi nolla. Positiivista 0 ja negatiivista 0 ei ole olemassa. Nollaa pidetään kuitenkin yleensä positiivisena. Tässä on positiivinen 0 ja negatiivinen 0 tämän tietyn muotokuvauksen vuoksi. Lukurivillä (katso yllä) voi olla myös +0 ja -0, mutta vain yksi nolla on olemassa.
64-bittinen liukulukumuoto
64-bittinen liukulukumuoto on samanlainen kuin 32-bittinen muoto, mutta siinä on seuraavat erot:
- Numeroa edustaa 64 bittiä.
- Etumerkkibitin jälkeen eksponenttiluvulle on 11 bittiä.
- Eksponenttinumero nollaindeksille (2 0 ) on 1023 10 = 01111111111 2 .
- Yksitoista bittiä seuraa 52 bittiä eksplisiittistä merkitsevyyttä varten.
- Siinä on laajempi numeroalue kuin 32-bittisessä muodossa.
Huomaa, että '1.' eli merkitsevyyden alussa ja ei vieläkään sisälly 64 bitin joukkoon, kuten se ei sisälly 32 bitin joukkoon 32-bittisessä muodossa.
Yksi tärkeimmistä eroista 64-bittisen ja 32-bittisen muodon välillä on se, että 64-bittisen muodon peräkkäisten sekamurtolukujen välinen ero on pienempi kuin 32-bittisessä muodossa.
64-bittisessä muodossa 1,0:n ja seuraavan sekamurto-osan välinen aikaväli (rako) voidaan laskea seuraavasti:
1.0 on
0 011111111111 00000000000000000000 00000000000 0000000000000000000000 2
Tämä vastaa arvoa '1.', jota ei ole merkitty merkkijonoon, kerrottuna 2:lla korotettuna potenssiin (indeksi) 0 (eksponentin ollessa 1023 10 = 01111111111 2 2:lle 0 = 1). Merkkijono on 1,0 x 2 0 .
Seuraava sekoitettu murtoluku, joka on suurempi kuin 1,0, on:
0 01111111111 00000000000000000000 00000000000 0000000000000000000001 2
Tämä vastaa '1'. jota ei ole merkitty merkkijonoon, jota seuraa 51 nollaa ja sitten 1, kerrottuna 2:lla potenssiin 0 (kun eksponentti on 1023 10 = 011111111112 2 2:lle 0 = 1). Tämä on sama kuin:
+2 0 × (1 + 2− -52 ) ≈ 1,0000000000000002
≈ tarkoittaa suunnilleen yhtä suurta kuin.
Nyt:
1,0000000000000002 – 1,0 ≈ 0,00000000000000002
Vastaava intervalliarvo 32-bittiselle muodolle on 0,0000001192092896 ≈ 0,00000012.
0,0000000000000002 on paljon pienempi kuin 0,00000012. Kahden peräkkäisen kokonaisluvun (esim. 3 ja 4) välillä on siis paljon enemmän sekoitettuja murtolukuja 64-bittisessä muodossa kuin kahden peräkkäisen kokonaisluvun välillä 32-bittisessä muodossa.
Kahden peräkkäisen kokonaisluvun välisten sekamurtolukujen määrä lukurivillä on ääretön. Mikään muoto (esim. 32-bittinen tai 64-bittinen) ei siis pysty tarjoamaan kaikkia sekoitettuja murtolukuja minkä tahansa kahden peräkkäisen kokonaisluvun välillä (kokonaislukuja). Mitä pienempi ero (väli) on muodon (esim. 32-bittinen tai 64-bittinen) tarjoaman kahden peräkkäisen kokonaisluvun välillä, sitä suurempi on sekoitettujen murtolukujen määrä peräkkäisten kokonaislukujen välillä (lukuriville).
Syyt siihen, miksi 64-bittistä muotoa kuvataan kaksinkertaisena tai korkeampana tarkkuudella 32-bittiseen muotoon verrattuna, ovat se, että kahden peräkkäisen sekamurtoluvun välinen aika, jotka rajataan kahdella peräkkäisellä kokonaisluvulla 64-bittisessä muodossa on pienempi kuin vastaava 32 -bittimuotoinen intervalli. Lisäksi kahden rajatun kokonaisluvun välillä on enemmän mahdollisia sekamurtolukuja 64-bittisessä muodossa kuin vastaavasti 32-bittisessä muodossa.
Desimaaliluvun desimaaliosan (murto-osan) muuntaminen binääriosaksi
36,375 on desimaaliluku, jonka desimaaliosa on '.375'. '.375':n desimaaliosa on nollan ja yhden välinen murto-osa. 0,5 peruskymmenessä on sama arvo kuin 1/2 kakkosarvossa. 0.5 10 joka ilmaistaan kahdella peruslaajennuksella on:
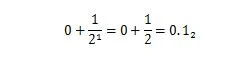
Se ei ole 0,101 2 mikä tarkoittaa 0,625 10 . Desimaaliluvun desimaaliosalla on vastaava binääriosa vastaavalle binääriluvulle. Joten muuntaaksesi desimaaliluvun, kuten 36.375 10 kahdeksi perustaksi muunna 36 binääriksi ja sitten 0,375 myös binääriksi. Yhdistä sitten molemmat tulokset binääripisteeseen. Menetelmät näiden kahden osan muuntamiseen ovat erilaisia. Miten desimaalikokonaisluku muunnetaan kantaluvuksi 2, selitetään luvussa 1.
Voit muuntaa desimaalimurtoluvun binäärimurtoluvuksi seuraavasti:
- Kerro desimaaliluku (desimaaliosa) kahdella. Tästä saatava kokonaisluku on ensimmäinen binääriluku.
- Toista edellinen vaihe desimaaliluvulla saadaksesi seuraavan binääriluvun.
- Jatka edellisen vaiheen toistamista, kunnes desimaaliluku on .0000—.
Esimerkki: Muunna 36,375:n murto-osa 10 vastaavaan murto-osaan kahdessa.
Ratkaisu:
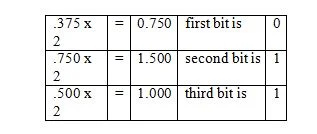
Huomaa, että kolmannessa vaiheessa 0,500 kerrottiin kahdella eikä 1,500. Vastaava binääriluku luetaan viimeisestä sarakkeesta ylhäältä. Ja niin, tulos on seuraava:
.375 10 = .011 2
Binääriluvun binaariosan (murto-osan) muuntaminen desimaaliosiksi
Tämän saavuttamiseksi laajenna binäärilukua 2:n käänteispotensseissa.
Esimerkki: Muunna 100100.011:n murto-osa 2 vastaavaan murto-osaan kantaluvussa kymmenen.
Ratkaisu:
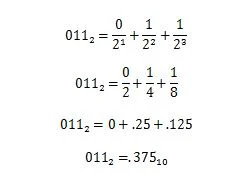
3.10 Numeroiden etuliitteet tietojenkäsittelyssä
Normaalissa elämässä 1 kilo tarkoittaa 1000, joka on lyhennetty k (pienet kirjaimet) kuten 1 kg. Laskennassa 1 kilo tarkoittaa kahta 10 = 1024, mutta se on lyhennetty K-kirjaimella (isoilla kirjaimilla) kuten 1Kbitissä. Normaalissa elämässä 1 mega tarkoittaa 1 000 000, joka on lyhennetty kirjaimella M (isot kirjaimet), kuten 1Mg. Laskennassa 1 mega tarkoittaa kahta kaksikymmentä = 1 048 576 = 2 10 x 2 10 = 1024 x 1024 = 1 048 576 ja se lyhennetään edelleen M-kirjaimella (isoilla kirjaimilla) kuten 1 Mbitsissä. Normaalissa elämässä 1 giga tarkoittaa 1 000 000 000 lyhennettynä G (isoilla kirjaimilla) kuten 1 Gg. Laskennassa 1 giga tarkoittaa kahta 30 = 1 073 741 824 = 2 10 x 2 10 x 2 10 = 1024 x 1024 x 1024 = 1 073 741 824 ja se lyhennetään edelleen G:llä (isoilla kirjaimilla), kuten 1 Gbit:llä. Seuraava taulukko antaa neljän etuliitteen merkityksen normaalissa elämässä ja tietojenkäsittelyssä:
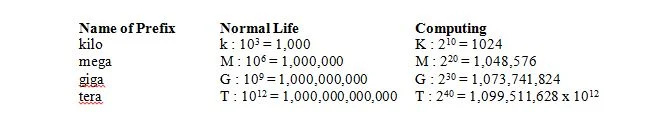
3.11 Ongelmat
Lukijaa kehotetaan ratkaisemaan kaikki luvun ongelmat ennen siirtymistä seuraavaan lukuun.
- Piirrä numeroviiva kokonaisluvuilla -10 - +10.
- Lisää seuraavat binääriluvut 8-bittiseen kahden komplementtiin: 101010 2 ja 1111 2 .
- Käytä vain kahden komplementin lähestymistapaa 8-bittisenä binääriluvun 1111 vähentämiseen 2 binääriluvusta 101010 2 .
- Etsi tuote 10110 2 x 1101 2 kahdessa pohjassa.
- Jako 36 375 10 1000 mennessä 10 desimaali- ja binäärimuodossa ja vertaa tuloksia.
- Käytä valitsemaasi 8-bittiä havainnollistamaan loogista AND-, TAI-, XOR-, Invert-, Shift Right-, Shift Left-, Rotate Right- ja Rotate Left -toimintoa. Jokaisessa tavussa tulee olla sekoitus ykkösiä ja nollia.
- a) Kirjoita nollan ASCII-merkin numeerinen koodi heksadesimaali-, binääri- ja desimaalimuodossa.
b) Kirjoita ASCII-merkin '1' numerokoodi heksadesimaali-, binääri- ja desimaalimuodossa.
c) Kirjoita 'A':n ASCII-merkin numeerinen koodi heksadesimaali-, binääri- ja desimaalimuodossa.
d) Kirjoita 'a':n ASCII-merkin numeerinen koodi heksadesimaali-, binääri- ja desimaalilukuina. - Muunna 49,49 10 kahdeksi pohjaksi. Muunna tuloksesi IEEE 32-bittiseen liukulukumuotoon.
- a) Miten IEEE:n 64-bittinen liukulukumuoto eroaa 32-bittisestä?
b) Anna kaksi toisiinsa liittyvää syytä, miksi 64-bittistä formaattia kuvataan kaksinkertaisena tai korkeampana tarkkuudella kuin
32-bittinen muoto.